绝对值编码器设计：是選磁编码器还是光学编码器

  磁位置编码器的角度分辨率和精确度与径向的磁铁扫描霍尔传感器的中心有关，受限于可行的插补细分深度和有效的磁场质量。通过每旋转扫描多个正弦周期，光学位置编码器具有更高的分辨率。如果使用磁码盘，这种方法也适用于磁编码器系统，但是哪个系统更好？

  本文描述磁和光学单芯片编码器的关键参数，权衡两种解决方案和比较两种编码器的性能来达到选择设计方案的目的。        

           目录

1. 介绍

2. 两种传感器，两种系统

3. 线性应用

4. 比较两种旋转编码器应用系统

4.1）装配公差和补偿特性

4.2）可能的误差来源

5.结论：哪个更好？

1）介绍

  如今的绝对位置传感器的制造需求与测量精度以及尺寸大小均和成本有关，而且往往及其多样化。好的选择是找到仅有的一个恰当的系统解决方案来适应手头的任务。所要解决的问题是耗时的，由于不仅是传感器的机械结构，而且每个没有体现在元件规格书里的的参数也要考虑进来。另外，开发集成传感器芯片必须基于一个给定的测量装置，或者提供合适可能的匹配。

  光学扫描器通常使用单独封装，方便对光电二极管阵列进行几何修改。然而，对于磁的霍尔编码器不具有可比的有效选项，为此不得不提供一个合适的传感器阵列在芯片内部，或者采用其他方法，由芯片布局决定磁铁的指标。小的外形尺寸和最佳性能通常是这两种解决方案都具有挑战性的设计目标。本文比较一个16管脚DFN封装的18位磁单芯片霍尔编码器iC-MU和一个optoQFN封装的18位光学编码器iC-LNB。

2）两种传感器两种系统

  多通道光电子扫描器iC-LNB捕获绝对位置数据用于线性位移测量系统或者旋转编码器（图1）。同步扫描一个10位二进制码，附加一个模拟的信号轨道用来评估实时的插补细分，使用一个小的编码量来达到高的角度分辨率。期望得到的绝对值位置和增量位置分辨率使用内部的算法得出，提供1至65536范围内任意脉冲数量的分辨率供选择。

     图1.光扫描器iC-LNB

  编码窗口宽度仅5.2mm，支持使用较小的码盘或者较大直径的空心轴。伴随着节能的iC-SN85 LED来担当一个紧凑的光源和iC-LNB的监视器，以及控制照度的级别。关键的逻辑处理也由iC-LNB内部执行，而更复杂的任务也可由一个外部的微控制器执行。

  偏置和幅度补偿功能已被集成到芯片内部，用于修正模拟轨道信号，这些信号也由差分的1024个周期的正弦和余弦信号通过四个输出端口输出。由信号矫正电路来降低插补细分的误差并获得更高的位置数据精度。

位置数据输出可以是并行的（高达16位）或者是串行的（使用一个快速移位寄存器）。时钟速率高达16MHz，允许循环读出时间小于1us。3.3V兼容的SPI端口支持器件设置和用来扫描位置数据以及诊断消息（例如，当奇偶校验位打开，存储监视标志一个错误）。最大允许速度依赖于分辨率；当17位分辨率时可获得6000rpm（表1）。

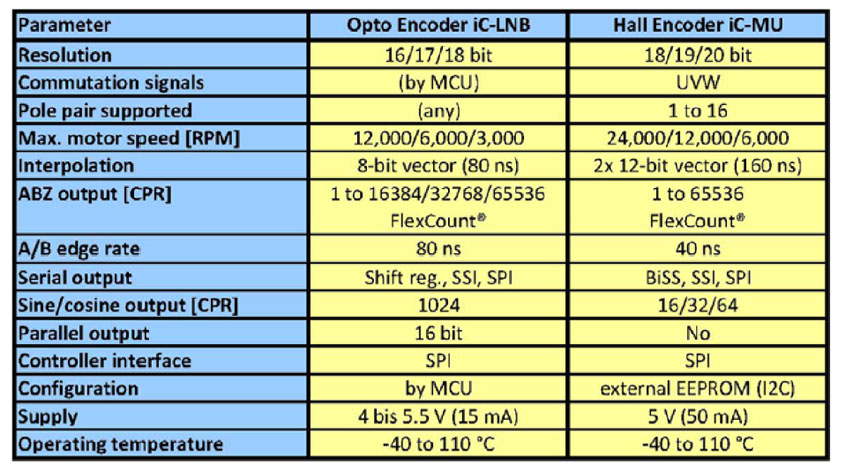
表1：元件电气参数

  霍尔编码器iC-MU是一个全集成的单芯片器件，是理想的磁码盘、磁鼓和磁带扫描器，适用于运控控制应用。典型应用包括绝对位置编码器、增量编码器以及用于无刷电机的换向编码器（图2）。位置数据被实时捕获并由串行接口（BiSS,SSI以及SPI）和一个增量接口两同时输出。任意数量的分辨率脉冲数可以使用内部"FlexCount"算法再次选择。

  采用合适的磁测量机构，设有两个增量轨道，极宽大约1.28mm，每个磁极对是差分的，由另一个磁极对交叉穿过测量间隔。两个同步的正弦-数字转换器用来数字化霍尔传感器信号；这些矢量跟踪转换器跟踪磁场变化率达8 MSPS，无延时。

  由两个轨道信号之间的相位差，集成的掩膜-已编程信号处理器计算绝对位置基于游标原理。使用这个原理，运动控制不必要获得绝对位置。在旋转应用中，可获得一个19位的分辨率（相当于2.5弧度秒），当使用磁码盘 MU2S 30-32时，以及支持的速度高达12000 rpm。

  通过安排磁极对在一个高分子磁铁上面的一个扁平码盘，可建立一个紧凑的系统，它可以理想的直接安装到电机的法兰上。扫描工作距离于芯片平面大约0.4mm。

  设计于一个16脚的DFN封装，iC-MU集成全部的所需编码器功能在最小可能的空间，仅5*5mm。偏心或者偏轴放置支持空心轴用于高分辨率的磁绝对值编码器。适合的磁码盘直径为30mm，支持空心轴直径高达10mm。

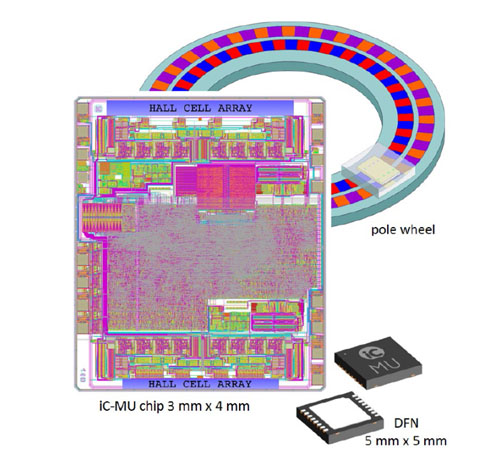
图2：磁传感器芯片和磁码盘

  通过设置细分因数从1到65536，数字角度位置可以从ABZ接口以任何分辨率输出。由于内部的“FlexCount”算法，整个范围的分辨率参数仅使用一只传感器就可以满足。这允许一个设计适合各种编码器分辨率而无需改变测量装置。完全安装好编码器的位置以后也可以编程，以最少的时间交付上市。而且，零位置信号也可以在装配好以后再编程。

  iC-MU可以产生3个换向信号（U、V和W）来运转无刷直流电机，适合电机极对从1到16。由于精确的电子调节UVW信号可以按照转子的位置改变而提供了一个关键的优势，使得不再需要通常使用的霍尔开关系统。

  由于可以支持空心轴应用，可以使用一个兼容的装配替换旋转变压器。作为整个系统的一部分，这将导致一个更便宜的旋转变压器替换解决方案产生，随着它的高分辨率，支持更精确的电机控制。

  SPI接口可以直接连接到一个微控制器，BiSS用于双向通信和CRC校验的超长距离通信，以及SSI是一个标准的编码器接口。所有的接口允许时钟频率高达10MHz。

  关于数据输入，iC-MU在BiSS协议下支持多从机应用链式连接，使用同步时钟连接多个编码器来捕获数据。如果一个相关编码器已连接并设置和开始工作，绝对精度有可能在最高速度时记录、评估以及由一个微控制器校正，这个微控制器可允许在系统中担当一个交互的输出接口。

3）线性应用

  iC-MU支持40，80，或者160mm距离的绝对线性测量，位置分辨率大约160nm。两个器件可被级联用于更大的距离，使得最大可能的测量绝对距离延长，由2到64的一个因数确定（图3）。这使得绝对距离测量系统可以达到数米，测量速度高达16m/s。

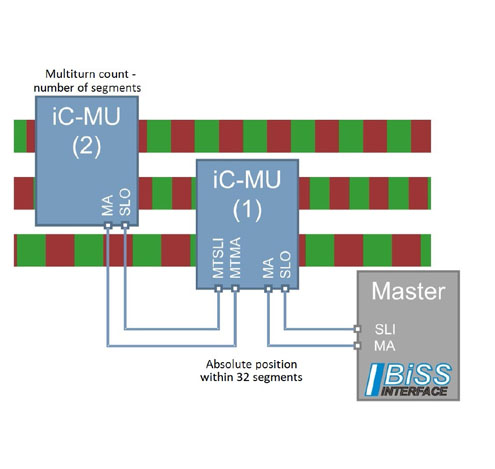
图3：元件级联用于线性测量系统和大空心轴应用

  例如，决定图3的多圈设计绝对位置测量来自于中间轨道的1024个循环和上面轨道的1023个循环。相位差由横跨整个2.6米的测量长度决定。下面的这颗iC-MU(1)在中间轨道的1024个循环和下面轨道的992个循环之间计算相位差。此装置因此重复产生32次位置数据，横跨整个测量长度。 多圈数据来自于iC-MU（2），用来区分这32个段。

  此外，级联两个iC-MU霍尔编码器，其他多圈传感器（齿轮箱）也可以用来提供它的多圈数据给iC-MU。一旦供给电源，多圈数据自动读取，并且在计量模式期间周期性检查。

4）比较两种旋转编码器应用系统

  两种编码器的传感器结构已经确定，支持小尺寸和成本敏感的产品而没有牺牲任何测量精度（图4）。尽管这两种器件采用不同的电路设计方法，它们同享类似的性能特性（表1）；支持任意可编程脉冲数的实时高绝对值和增量信号分辨率。

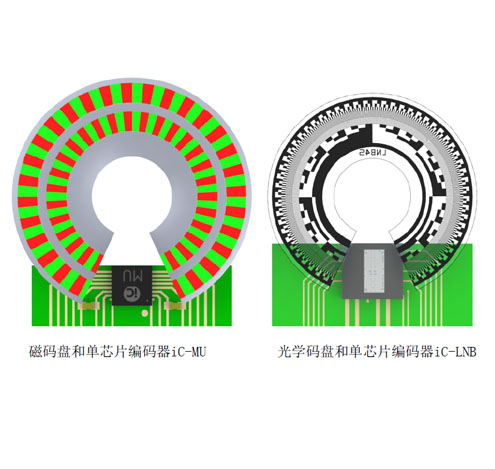
图4：装配原理和尺寸比较

  当选择基本的系统布局时其他决定因素也必须考虑进去，例如应用领域和测量精度要求。表2比较了主要的传感器规格参数。

表2：光和磁传感器的特征比较

  随着完美的电子处理测量系统，磁码盘的磁极间距误差是绝对测量误差的显现来源。例如，一个典型的磁精度是15um，而光学码盘的线精度是300nm，差别是显而易见的。借助于扫描半径（表3），这个值可以被转换成角度误差；在理论上，磁编码器系统大约为0.07°（252弧度秒）以及光编码器系统大约为0.0018°（6.4弧度秒）。光学系统其它的主要误差来源总计为0.011°（40弧度秒）。

  用户选择一个特定的系统主要依据这个系统的优点和缺点。例如，磁编码器系统具有多种优势的环境免疫力，诸如，灰尘、油污以及水汽。它也允许一个宽的工作距离，允许轴向间隙和安装公差较大而容易装配。由于磁编码器系统无需LED和光学器件，一个扁平的编码器设计成为可能，1Ω时产生的信号电压为200mV。

  对于磁传感器，磁场分量垂直于芯片是有益的。霍尔效应直接提供一个典型的mV级电压，依赖于磁场强度分量Z。由于单个霍尔元件仅能感知到磁铁的距离，而采用多个霍尔元件在不同位置记录磁场的Z分量以便角度信息可由各个局部的磁场渐变得出评估。霍尔元件必须真实地"感知"这个弯曲的近场磁力线。由于霍尔电压的极性跟随磁场的方向，磁铁的北极可区别于南极，使得使用一个极对来确定绝对角度成为可能。

  霍尔元件最多仅能从磁码盘的磁场产生10mV的电压。为了达到光学编码器系统的分辨率，信号的带宽必须被限制。为了达到信号调理的目的，霍尔元件使用一个固定的扫描频率和滤波来评估。这个霍尔传感器扮演了一个模拟低通角色，截止频率大约20kHz。然而，实际上，较长的信号传输延时是不相关的。

4.1）装配公差和补偿特性

  两个系统都使用快速实时插补细分电路由向量追踪转换器使用arc tangent进行转换。关于偏置、幅度匹配、相位精度和谐波，此转换器依赖于模拟的正弦/余弦传感器信号。然而，与理想的装配位置的偏差引起的信号误差会减小插补细分的精度。为了确保测量精度，两个系统都允许静态校准由装配引起的信号误差和通过集成的D/A转换器校正调节几个模拟信号路径。

  电子信号校准会增大机械活动限制度（表3）。iC-MU也允许正弦/余弦相移校准，这也能补偿径向对准误差。一旦设置和校准，所选择的工作点由自动功能来维持。对于光学编码器，集成的LED功率控制补偿由温度上升引起的LED效率损失。霍尔编码器有一个增益控制用来补偿当磁码盘与芯片距离的变化时引起的场强改变。

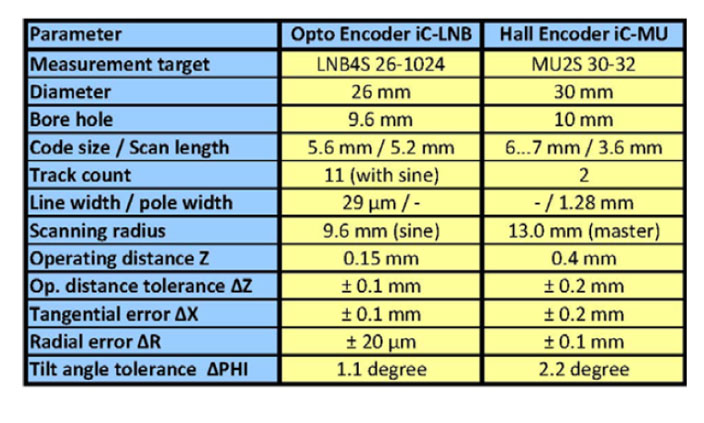
表3：机械数据和装配公差

4.2）可能的误差来源

  原则上，误差应该被通盘考虑进去。在这里，已对基本情况进行了考察，拿霍尔编码器作为一个例子。如果测量用磁铁的相关几何尺寸已被考虑进去，这些考察结果也同样适用于光学编码器系统。

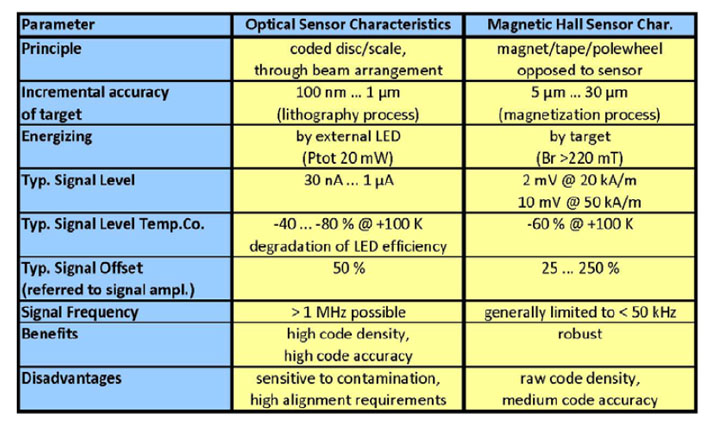
  如果霍尔编码器在扫描半径对齐不理想，将会引起正弦信号失真。如果有一个半径位移（ΔR），霍尔元件不能探测到磁体或者探测到分段的磁极不在正确的位置（图5B）。正弦和余弦信号就会有一个固定的位移误差在随后的扫描中出现。然而，这也可能通过使用集成的信号校正电路得到补偿。

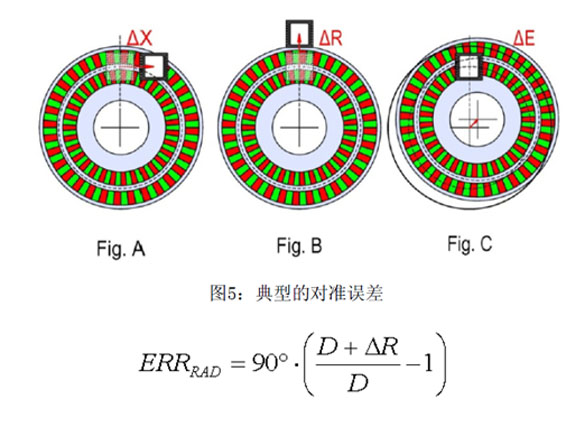
表达式1：由于径向对准引起的测量误差

  表达式1给出了传感器信号电子相位误差，D为扫描直径，ΔR为扫描位移。例如，参考电子正弦周期信号，一个霍尔编码器径向0.1mm位移会产生0.35°的相移在扫描直径为26mmm时。如果计算每旋转的机械角度误差，结果必须除以极对数。一个标准磁码盘有32个极对，相当于机械角度误差为0.01°。

  另一方面，器件在切线方向的位移（ΔX）对两个轨道信号电子角度相移的影响或大或小是相同的（图5A）。这个间距改变和相位差异仅轻微地影响计算绝对位置值，实际上几乎不会改变。

然而，偏心装配误差（ΔE）会引起设备抖动（图5C）。直径越小，测量目标的改变越大。一个长波误差出现会减小绝对测量精度。

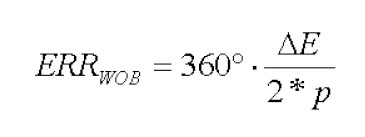
表达式2：由偏心率引起的测量误差

 偏心率误差来自于测量器件的位移ΔE，这个误差来自于旋转轴和测量磁铁的极宽p。因此，一个偏心率10um的误差导致相位误差为1.4°（参考正弦周期），或者角度误差0.05°;（参考机械旋转），有关尺寸大小，见表3，扫描直径26mm，极宽1.28mm，32极对。对于起决定性作用的相位差游标计算，偏心率误差扮演着一个较小的影响，由于两个信号轨道的偏心率是相同的。

在一个完整的机械旋转360°，角度精确度优于+/-0.1°。这个精度受磁化系统的限制。如果个别的磁极变化，轻微的位移影响在大约45°和90°如图6所示。连接参考编码器的机械轴也产生一个轴心误差，它可以通过在同一个方向旋转的一个长波偏离观察到。

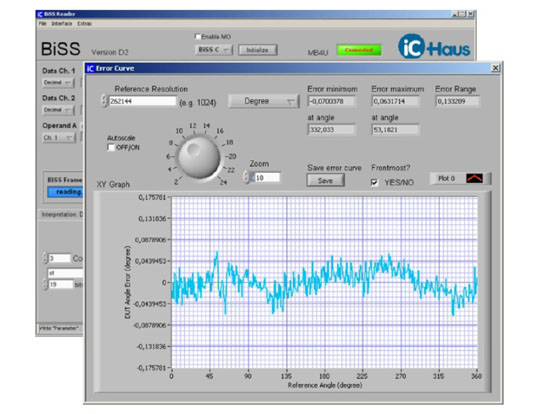
图6：iC-MU磁系统角度精度

图6展示了iC-MU磁系统的角度测量精度，使用磁码盘 MU2S 30-32，周期角度为11.25°。在这里，数学和图形功能在BiSS读出软件里能容易的比较测量数据。

5）结论：哪个更好？

  磁传感器技术有很多优点可说：优秀的可靠性、对冲击和振动的高抵抗性、不易碎、对灰尘和水蒸气不敏感。单芯片霍尔编码器iC-MU允许使用空心轴以及可实现仅有光编码器才能做到的位置分辨率。然而，对于高测量精度的应用，光学传感器，诸如iC-LNB等有优势，但是需要更昂贵的装配成本。但是，考虑到它们具有小的optoQFN和optoBGA封装，单芯片编码器是一个可行的选择。基于这些关键点，决定选择哪一个方案应该由应用本身的需求来决定。